[algorithm] 알고리즘 04 : 그래프 알고리즘
그래프의 구조
- 정점(vertex) : 그래프에서 표현하는 항목. 지하철 노선도의 역
- 간선(edge) : 두 항목 사이의 관계. 지하철 노선도의 역과 역을 연결 하는 선
그래프 탐색 알고리즘
→ 그래프의 모든 정점들을 체계적으로 방문하는 알고리즘
- 깊이 우선 탐색(depth first search)
- 너비 우선 탐색(breath first search)
그래프의 표현
- 그래프의 종류
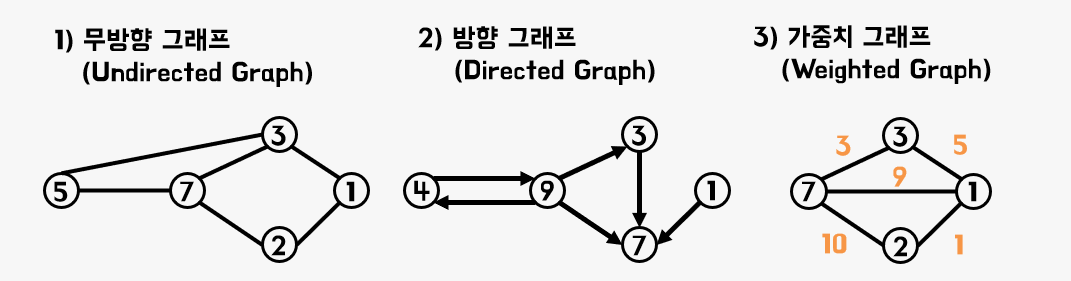
-
사진 출처 : https://laboputer.github.io/ps/2017/09/29/graph/ 괭이쟁이 블로그
- 무방향 그래프(undirect graph)
- 간선들이 어떠한 방향을 가지지 않음
- 간선 e = (u, v), 간선은 e , 각각의 정점은 (u, v)로 표현
- e는 (u, v) 혹은 (v, u)로 표현하여도 동일한 간선을 의미한다.
G = (V, E)
V = {1, 2, 3, 5, 7} : 정점의 갯수
E = {(1,2), (1,3), (2,7), (3,5), (3,7), (5,7)} : 간선의 갯수
- 방향 그래프(direct graph)
- 간선들이 방향을 가짐
- 한 간선 e가 정점 u에서 시작하여 정점 v에서 끝날 떄, e = (u, v)
- 반대로 정점 v에서 시작하여 정점 e에서 끝날 떄, e’ = (v, u)
G = (V, E)
V = {1, 2, 4, 9} : 출발 지점
E = {<1,7>, <3,7>, <4,9>, <9,3>, <9,4>, <9,7>} : 화살표의 갯수
- 가중 그래프(weighted graph)
- 비방향(또는 방향) 그래프의 간선에 가중치(비용)를 부여한 그래프
- 가중치는 친밀도의 크기, 도시간의 거리, 가스파이프라인의 두 지점 사아의 용량, 지하철 역 사이의 소요 시간 등을 나타낼수 있음
- 연결 그래프(connected graph)
- 그래프 G의 두 정점 u와 v사이에 모든 정점들이 연결된 그래프
- 비연결 그래프(disconnected graph)
- 그래프 G의 두 정점 u와 v사이에 모든 정점들이 연결되지 않은 그래프
- 무방향 그래프(undirect graph)
- 순환
- 그래프 G의 두 정점 V1 와 Vn 사이의 경로 : { V1, V2, V3 … Vn }
- 위 그림 가중 그래프의 정점 3과 정점 2 사이의 모든경로 : {3,1,2}, {3,7,2}, {3,1,7,2}, {3,7,1,2}
- 두 정점의 경로를 구성하는 간선의 수를 경로의 길이라고 한다.
- 경로 { V1, V2, V3 … Vn }에서 V1 = Vn 이면 이 경로는 닫혀있고 이러한 경로를 닫힌경로라고 한다
- 3개 이상의 간선을 가지고 경로에서 어떤 간선도 중복되지 않은 닫힌경로 일때 순환이라고 한다.
- 이러한 순환을 가지는 그래프를 순환그래프라고 하고 순환이 없는 그래프를 비순환그래프 라고 한다.
- 위 그림 가중그래프애서 {1,2,7,3,1}, {1,7,3,1}은 순환이다. 따라서 위 가중 그래프는 순환그래프인다.
그래프의 컴퓨터 프로그램 표현
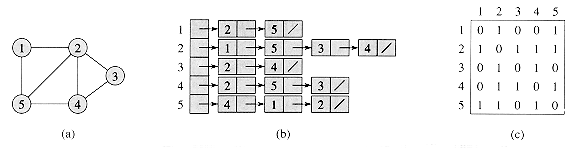
- 사진 출처 : https://devhwan.tech/54 5분개발
- 인접 목록(adjacency list)
- 그래프의 각 정점의 이웃 정점들을 연결목록(linked list)으로 표현하는 방법
- 각 정점에서 갈수 있는 정점들을 간선들을 표현
- (b)와 같이 5개의 연결목록 이 존재
- 해당 연결목록에 있는 노드들의 수는 5(정점들의 수) + 7(간선들의 수) = 12 이다.
- 인접 목록은 간선들의 수가 적은 저밀도 그래프를 표현하기에 적합함
- 가중치 그래프에서는 각 연결 목록의 간선((u,v)) 마다 가중치의 값 (w(u,v))을 저장한다.
- 인접 행렬(adjacency matrix)
- 그래프내의 두 정점들 사이에 간선이 있는지를 행렬로 표현한 것
-
aij = ${1, 정점 i와 정점 j 사이에 간선이 있는 경우 \brace 0, 정점 i와 정점 j사이에 간선이 없는 경우}$
- 무방향 그래프의 경우 aij = aji 는 같다. 행렬의 구조가 대칭을 이룬다.
- 인접 행렬은 작은 그래프나 고밀도 그래프를 표현하기 위해 사용된다.
- 각 정점의 사이에 간선이 있는지 빨리 알수 있다.
- 가중치 그래프에서는 1대신 가중치의 값 (w(u,v))이 들어간다.

Comments